Число Нараяны

Число Нараяны — число, выражаемое через биномиальные коэффициенты ([math]\displaystyle{ k\leqslant n }[/math]):

[math]\displaystyle{ N(n,k) = \frac{1}{n}{n\choose k}{n\choose k-1} }[/math];

такие числа формируют треугольник Нараяны — нижнюю треугольную матрицу натуральных чисел, возникающую в ряде задач перечислительной комбинаторики.

Открыты канадским математиком индийского происхождения Тадепалли Нараяной (1930—1987) при решении следующей задачи: найти число коров и тёлок, появившихся от одной коровы за 20 лет, при условии, что корова в начале каждого года приносит тёлку, а тёлка дает такое же потомство в начале года, достигнув возраста трёх лет.

Первые восемь рядов чисел Нараяны:

k =       1   2   3   4   5   6   7   8
n = 1  |  1
    2  |  1   1
    3  |  1   3   1
    4  |  1   6   6   1
    5  |  1  10  20  10   1
    6  |  1  15  50  50  15   1
    7  |  1  21 105 175 105  21   1
    8  |  1  28 196 490 490 196  28   1

Приложения и свойства

Пример задачи подсчёта, решение которой может быть задано в терминах чисел Нараяны [math]\displaystyle{ N (n, k) }[/math], — это число выражений, содержащих [math]\displaystyle{ n }[/math] пар круглых скобок, которые правильно сопоставлены и которые содержат [math]\displaystyle{ k }[/math] различных вложений. Например, [math]\displaystyle{ N(4,2)=6 }[/math] как четыре пары скобок образуют шесть различных последовательностей, которые содержат два вложения(под вложениями подразумевается шаблон ()):

()((()))  (())(())  (()(()))  ((()()))  ((())())  ((()))()

Пример демонстрирует, что [math]\displaystyle{ N(n,1) = 1 }[/math], так как единственный способ получить только один шаблон () — [math]\displaystyle{ n }[/math] открывающих скобок, а затем [math]\displaystyle{ n }[/math] закрывающих. Также [math]\displaystyle{ N(n, n)=1 }[/math], поскольку единственным вариантом является последовательность ()()() … (). В более общем случае можно показать, что треугольник Нараяны обладает следующим свойством симметрии:

[math]\displaystyle{ N(n,k)=N(n,n-k+1) }[/math].

Сумма строк треугольника Нараяны равняется соответствующим числам Каталана:

[math]\displaystyle{ N(n,1) + N(n,2) + N(n,3) + \cdots + N(n,n) = C_n }[/math],

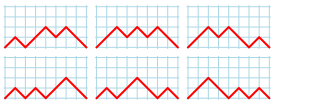
таким образом, числа Нараяны также подсчитывают количество путей на двумерной целочисленной решётке от [math]\displaystyle{ (0, 0) }[/math] до [math]\displaystyle{ (2n, 0) }[/math] при движении только по северо-восточной и юго-восточной диагоналям, не отклоняясь ниже оси абсцисс, с [math]\displaystyle{ k }[/math] локальными максимумами. Фигуры получающиеся при [math]\displaystyle{ N(4,k) }[/math]:

[math]\displaystyle{ N(4,k) }[/math]	Пути
[math]\displaystyle{ N(4,1)=1 }[/math] путь с одним максимумом:
[math]\displaystyle{ N(4,2)=6 }[/math] путей с двумя максимумами:
[math]\displaystyle{ N(4,3)=6 }[/math] путей с тремя максимумами:
[math]\displaystyle{ N(4,4)=1 }[/math] путь с четырьмя максимумами:

Сумма [math]\displaystyle{ N(4,k) }[/math] равна 1 + 6 + 6 + 1 = 14, что равно числу Каталана [math]\displaystyle{ C_4 }[/math].

Производящая функция чисел Нараяны:

[math]\displaystyle{ \sum_{n=0}^\infty \sum_{k=1}^n N(n,k) z^n t^k = \frac{1+z(t-1) - \sqrt{1-2z(t+1)+z^2(t-1)^2}}{2z} }[/math].

Литература

• P. A. MacMahon. Combinatorial Analysis (неопр.). — Cambridge University Press, 1915–1916.
• Petersen, T. Kyle. Narayana numbers // Eulerian Numbers (неопр.). — Basel: Birkhäuser, 2015. — doi:10.1007/978-1-4939-3091-3.